搭訕要像光一樣地移動

各位有在路上搭訕的經驗嗎？

據說現在鮮少人這麼做了，很大一部分是大家都在低頭玩手機(還有個搖一搖就能搭訕的軟體，這種輕鬆方便到令人忌妒的功能，真是污辱了古早時期搭訕者的勇氣與決心)，沒什麼人抬頭四處張望。

安排命中注定的情侶擦身而過，結果一個在上臉書一個在玩小遊戲，連月下老人都不知道該怎麼辦。

真遺憾。

錯過的搭訕

古早味的搭訕，通常發生在等朋友、等公車、等紅綠燈，站在某個地方等待的時候。想像你站在廣場一隅，攘往熙來的行人，形成兩道南北反向的河流，緩緩流經廣場。

瞬間，站在東南角的你胸口一緊，你瞧見廣場西北角佇立著一位女孩，她以側面45度對著你，頭向下俯角20度，差不多是找地上有沒有銅板的角度，臉上掛著30度的笑容，露出一個深度0.3公分的酒窩，大約能裝下2毫升的依雲礦泉水。

你摸一下後腦，確認是否有破洞，不然，為什麼理想的她竟然從腦海中走出來了。你擦一下眼鏡，確認她沒有消失，不是你單身過久，強烈的思念將她的影像從眼睛裡投射到自己的鏡片灰塵上，比Google glass還先進。沒錯，她是真人，而且她剛還摳了一下鼻子，擦在電線杆上，她這個動作，美到簡直可以做成月曆銷量破百萬。

你注意到她抬頭看了一下對面的紅綠燈，一飛秒（femtosecond: 10的負十五次方秒，飛秒雷射的飛秒就是這個意思）內，你下了決定，你知道如果你沒行動的話，這輩子都將浸泡在絕望中。

走過去吧，就算最後一刻孬掉，你也可以像個變態一樣去摸電線杆！

你邁出步伐，越走越快，最後跑了起來，你想像自己像一道，沿著廣場對角線，筆直地衝向她。她過馬路，紅燈亮起，她消失在車流之後。你雖然想衝過去，但又怕在這條八線道上，一不小心連三途河都過就不妙了。

下個綠燈亮起，你趕過去，她已不知去向。

事後，你躲在自己的小房間裡，旁邊擺著一張擦過電線杆的衛生紙。你怨恨自己為什麼不早幾秒看見她，為什麼不敢衝過馬路。你祭出最狠的自我懲罰，拿出國中理化課本，全部習題重做一次，又無聊又嗜睡又還不大懂，沒有比這更殘酷的懲罰了。忽然，你瞥見課本上的一張圖，一股懊惱從啤酒肚湧上。

你發現你錯了，你沒有像光一樣地衝向她。

光都會拐彎

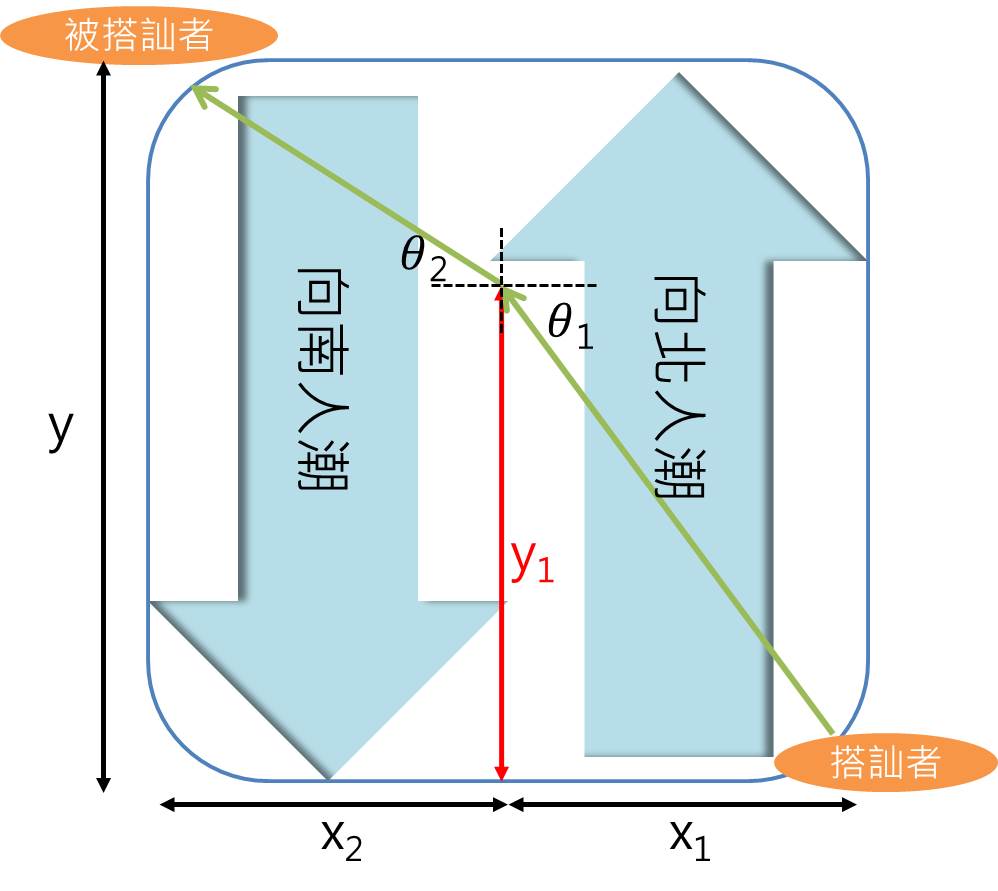
下圖是以數學角度描述的廣場示意圖：

首先，我們得知道，通過兩條人河的最快速度是不同的。好比逛夜市，忽然想吃另一側的攤位，要是那攤位在前面，你加快腳步就能快速抵達。但要是那攤位在後頭，你只能邊忍受其他人的白眼，邊緩慢地移動到那兒。

回到廣場上，當你往北跑，穿越往北人潮與穿越往南人潮的最快速度是不同的。你應該盡量在移動速度快的往北人潮中待久一點，以縮短移動時間。但偏偏最短距離又是對角線，路線偏離對角線越遠，得走越多路，移動時間因此增加。

假設你在往北與往南的人潮中移動的最快速度各自是v₁與v₂，往北與往南的人群寬度告自是x₁與x₂，在往北人群裡往北移動的距離為y₁，廣場南北的長度是y。利用三角形斜邊長為兩邊平方和開根號，移動時間為移動距離除以移動速度，我們可以算出移動所需的時間為

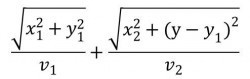
想調整y­₁以最小化移動所需的時間，盡快跑到夢中情人的身邊，我們得將上面的式子對y₁微分

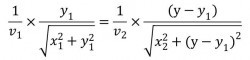
化簡後得到v1/v2 = sinθ₁/sinθ₂。如前圖所示，θ₁與θ₂是從第一道人群進入第二道人群時的入射角與折射角。這式子告訴我們，給定通過兩條人河的最快速度v₁與v₂，你必須要調整到進入不同人群時，入射角跟折射角比例等於速度的比例。這正是國中理化的司乃爾折射原理：經過不同物質，會產生折射。這才是光傳輸的真正路徑。一端在水中的筷子看起來像是斷掉一樣，正是司乃爾定律造成的。

要是你真的如同光一樣地追逐夢中情人的背影，有計算過最佳的折射角度，那你將會比原來更快抵達她的身旁。說不定，此刻你的衛生紙上已經寫著她的電話了。

你感覺到月下老人拿著理化課本，對你嘆了一口氣。

這一切，都是因為你國中理化課在打瞌睡。